A noob explains Bayesian epistemology

Come for the philosophy, stay for the curvy charts

Jan 02, 2024

The pitch

Let’s admit that we rarely, if ever, know something as stone-cold truth.* Typically, for a given topic, we associate some spectrum of opinion to it, and have a vague sense of our own assignment of certitude over that spectrum. Some opinion is very likely correct, others are less likely, still others are effectively ruled out. As we observe and reflect on the world around us, we often update our own assignment of certitude across this spectrum. And ultimately, if you ask us to make a decision, we’ll act based on this spectrum, perhaps for example on whatever opinion we are most certain, but knowing this is a practical choice only.

(*This premise may raise your hackles. Please notice I’m not saying truth doesn’t exist, I’m saying we aren’t ever sure we know exactly what it is.)

If this description of how we reason about truth resonates with you, you may be interested to hear it is a well-developed framework called Bayesian epistemology, after the mathematical theorem by Rev. Thomas Bayes. It certainly resonates with me, and I find once you reframe your own thinking this way, it’s hard to see things any other way (although like all frameworks it can only take you so far and I have my misgivings, which I’ll get into).

Although I’m no philosopher — so let’s explore it together, one noob to another. (At the end I’ll link some other references, of varying degrees of rigor.)

(By the way, I wrote a previous post about a thought within this framework. The purpose of the current post is to back up a little and provide a beginner-friendly intro to the basic idea.)

Example: aliens!

Consider your personal, internal belief model of whether aliens exist or not (which is probably muddled up with your belief model of what they look like, how likely it is that they’d appear on earth, et cetera, that’s fine for now).

I’m guessing you think aliens exist, somewhere, probably, give it like a 80% chance, but they probably won’t manifest themselves on Earth in our lifetime, give that like a 70% chance, they probably don’t look like little green men but maybe are observable entities not some freaky electron level ambience, errr like 50/50 on that one, et cetera.

These are your starting beliefs, your prior assumptions, or priors. They are shaped by all sorts of things: your own thoughts and prejudices, your friends, your environment.

Now:

Imagine that a tentacled alien being appears in your living room at this very moment, materializing from a vertical blue beam streaming ethereally from an obelisk spacecraft barely visible in the sky. The tentacle-man makes an unintelligible noise and you feel a strange sense of dread and your nose for some reason starts bleeding. This is evidence, observation, fact.

Your prior assumptions adjust. Before you even verify what the tentacle-man is, the nature of the obelisk or your bleeding nose, your internal model of things has adjusted. “Alien existence” has bumped to 95% (but not 100% because what if you’re just hallucinating??), and “aliens are observable” is at like 80% (not higher because you’re not sure if the being is actually the entity itself or just an avatar of some transdimensional intelligence). After adjusting your prior beliefs based on evidence, you have a posterior belief.

Does this all seem like a fair representation of your thought process?

If so, we can apply this to all sorts of situations: belief in the possibility of time travel, confidence that the roast beef sandwich will have mustard on it like you ordered, belief in the existence of God, opinions on a politician or colleague or lover, stance on a political issue or social policy. In each, you have some existing set of opinions (i.e. priors), through discussion or debate or experience you may encounter new ideas or observations which alter this opinion (i.e. evidence), leaving you with an updated view on that topic (i.e. posterior).

(Btw, I’m being very flip here, mentioning mustard in the same breath as the Almighty, to make the point this is a general framework for reasoning — please note however, obviously, “mustard” is a clear mostly binary and independent outcome, whereas “God’s existence and nature” is a belief tied to a life’s worth of interlinked other credences and decision-making.)

Forcing math onto this framework

I don’t think we need to force math onto this idea, at all. We’ve got an idea of prior beliefs, updated by evidence, giving posteriors. Those posteriors become our new priors, and on we go.

But it is quite beautiful that not only is there a mathematical model for all this, it’s one of the most fundamental theorems in all of probability. And because we have a math model, we could (in theory) quantify things like “credence” or “belief” or “likelihood” or “prior”. In reality, I personally think beliefs are too squishy to assign numerical values, and the model is useful as a framework only, but others disagree — but this is a follow-on, deeper topic. Let’s explore the math.

Enter: Reverend Bayes

Bayes’ theorem (attributed to the 18th century Presbyterian minister Rev. Thomas Bayes) tells us:

The probability of the posterior is proportional to the probability of the prior times the likelihood of the evidence (given the prior)

(Recall “a is proportional to b” means “a equals some constant times b”, or “a = c x b”. Imagine fixing, say, c = 3, then possible values for (a, b) are (15, 5), (6, 2), (36, 12), etc.)

To explore the more precise mathematical expression of this statement, we need to introduce a little notation.

Let P(A) represent “probability of event A”. For example, if we’re playing cards, let A be the event “drawing an ace”, and we have P(A) = 4 / 52 = 7.7%.
Let P(A|B) represent “probability of event A, given event B has happened”. For example, let B represent “holding an ace”, and we could say “given we’re holding an ace, the probability of drawing an ace”, P(A|B) = 3 / 51 = 5.9%.

(Similarly, P(B|A) would be “probability of B, given A has happened”.)

Now we can take a look at Bayes theorem, which says:

\(P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}\)

This puts in math notation the phrase from before.

P(A|B) — posterior probability of A, given B has occurred. (Posterior probability of aliens existing, given we just had a tentacle-man appear in our living room)
P(B|A) — likelihood of the evidence given our priors on A. (Likelihood the tentacle-man should appear, given our prior belief in aliens.)
P(A) — prior probability of A. (Your credence in aliens before the living room visit.)
*Feel free to skip this one* P(B) — marginal likelihood of the evidence. (The likelihood of having a tentacle-man appear in one’s living room, independent of any particular prior, personal belief in aliens.) This idea may feel a bit more dodgy. Note since this doesn’t depend on our belief in A, it’s a constant term with respect to A, so if we’re just interested in thinking about changes to A, we can sort of avoid it — noting that P(B) being constant means 1/P(B) is also constant, we can say “P(A|B) is proportional to P(B|A) times P(A)”, like we did in the word-definition before. *End skip opportunity*

It’s worth noting this theorem is derived directly from the 3 axioms of probability, and is completely uncontroversial on its own. It can become controversial, like all math formulas, when we start applying it to things.

Which we shall do now.

Another example (this time with graphs!)

Let’s try a very simple example, with coin flips. I’m going to do a more layman friendly version here of a recent slightly more math-y version I did on my other blog (check it out!) — and with a view here on the “Bayesian epistemology” topic.

(And btw, real life is not dice or coin flips or decks of cards, but we’ll get to that next.)

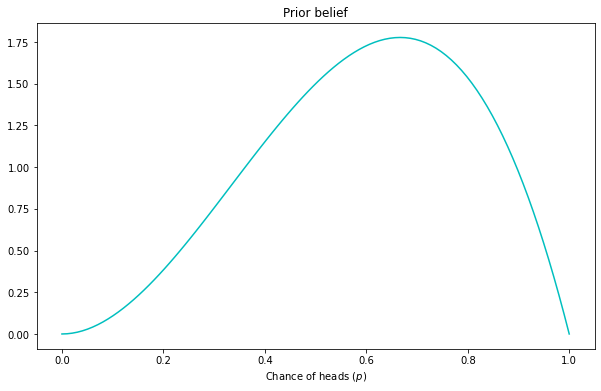
Say you’re at a shady casino, playing a game that involves a coin flip. Heads the house wins, Tails you win. Based on the shadiness of the venue, you come in with a prior belief the coin isn’t fair, that the heads side is loaded to come up more often. Specifically, you feel there is some underlying probability of the coin coming up heads, capturing its dimensions and balance, call it p, and you’re fairly certain p is more than 50% (aka unfair). (In the formula earlier, p is in the leading role of “thing A”.) If you had to represent your mental, personal prior on the coin’s head-probability p, it might look like:

In other words, you mostly think the coin is pretty unfair, coming up heads 60-70% of the time. But you’re not sure, there’s a possibility it’s fair, or even skewed toward the player if they made a mistake or something — this represents that smaller left “tail”.

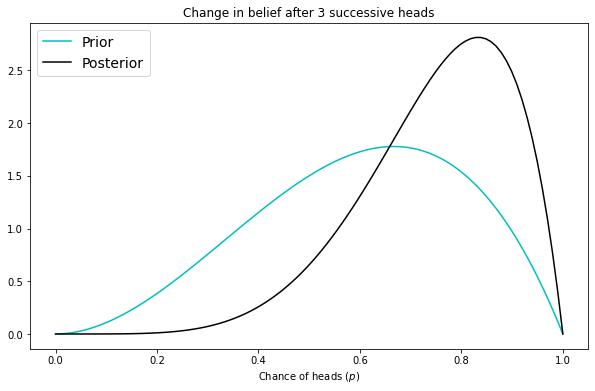
Now the dealer starts flipping. Heads, heads, heads. This is evidence (in the formula before, played by “thing B”). After this evidence, you update your prior, and have:

Our belief, credence, opinion about the coin being unfair is more sharp now that we’ve seen 3 heads in a row. Instead of just P(A), we now have P(A|B). We leave some room for it being an unlucky streak, we’re not 100% confident of any extreme, but we are growing very confident the coin is unfair, probably around 80-90% if we had to put a number to it. Important note: this streak of heads helped confirmed our prior, so the posterior moved our update pretty strongly. If we’d started with a different prior, say a belief that the coin was tails on both sides (with the graph looking skewed all the way to the left), it’d take a lot more heads to skew us back toward what we see above.

Again, this is all very intuitive to me, and matches how I think I and many people interact with uncertainty in the world, in general. Attaching exact numbers to it seems overkill, but the framework is brilliant.

Anyway, this posterior is now, in a sense, our new prior. We associate this new prior with the casino and move on with our lives.

We might recall the tentacle-man here — before we witnessed him, we had a prior over his existence similar to the coin flip — heads = aliens, tails = no aliens. Once he beamed into our living room, this updated. And think of someone who strongly believes aliens are a myth — upon seeing the same scene, they’d have a much stronger instinct to disbelieve their eyes or discount it as hallucination/etc — their posterior would look different than yours.

Life is not the casino

This example is, I hope, illustrative of the basic mechanics and intuition of Bayesian thinking. (Again, to dip your toe into a little more math-y version of this may I suggest this post. But we’re not here to talk math (sad).)

But, you may find this simple example raises more questions than it answers. Here’s two that come to my mind:

The variables of life are not as neat as the variables of a casino. In a casino, we have full knowledge of the rules of the game, the elements of chance are typically isolated (one die roll or card drawn at a time), and behave predictably. In life, we don’t know the rules, everything uncertain is connected to everything else, and it seems very little is predictable. Does the framework still work?
The variables of life are very mis-behaved, which doesn’t play well with Bayesian updates. By “mis-behaved”, I mean the very specific, mathematical fact that the Bayes theorem performs best when its subjects have finite variance and the prior can reliably converge given enough observations. This is what I explored in a previous post, but basically my concern is for so-called “fat tailed” randomness, where one extreme observation would wildly change our posterior, and we can’t dismiss that extreme as an outlier because we’re dealing with something that is inherently full of extremes: stock prices, wealth, nature (think insurance risks and acts of God), changes in complex systems, etc.

The problems that come to philosophers’ minds tend to be more “gotcha” feeling, to me, and are a little too technical for this post (read: I don’t understand them well enough to explain them). (For example, the Dutch book argument.)

Another thread that pops up a lot, both in epistemology and statistician circles, is the “problem of priors”. Choice of prior is very influential on your posterior, so it matters what you choose, and there are many cases where you can’t, or don’t want to choose a prior. In math, I agree this is a serious concern and rightfully attracts a lot of attention to address. As a personal epistemological framework, it seems like a feature not a bug — humans can’t come into any situation as a pure tabla rasa, we bring baggage even if we know nothing about what we’re considering, so it seems good to explicitly force a representation of this fact.

{ Notebook }

Discussion about this post