In this series of posts (if I can keep it going), I’ll explore different math concepts in a layperson-friendly but still mostly rigorous and detailed way.
A quick note on desired tone and audience. There are already lots of layperson-friendly pop-math YouTube channels and blogs (I’ll list a bunch at the end of this post). But a) I don’t think you can have too much of a good thing and b) most of these, especially the written stuff, avoids technical detail. My intended audience is a layperson with some technical bent (like, you took calculus and liked it but then majored in humanities).
So, I realize for mathematician readers this post will feel pedantic, and for completely math-averse readers I might lose you — that’s ok. I’m aiming to strike a balance here. And another motive is to make my own tiny contribution to shifting public perception of mathematics away from inane memes like 6 ÷ 2(1+2) = ? and toward meaningful (but accessible) examples of its essence and scope.
How math is made
In this first post, we’ll explore how to build up a field of math from a small set of axioms. By field of math think like “calculus”, or “geometry”. More specifically, we have things like differential geometry (the math behind Einstein’s relativity), or topology (a study of abstract structures), or as we’ll explore here, probability (the study of chance).
An axiom is a simple statement that we assume to be true without any demand for proof. Something like “a + b = b + a”, or “between any two points, we can draw a straight line”. From the axioms, we use logic to deduce new statements, which we call theorems (or postulates, or lemmas).
I previously explored this idea very briefly in a post contrasting mathematics as a deductive discipline, with science as a inductive discipline, using Euclidean geometry and the axioms laid out in The Elements. For this post, I’ll use probability theory.
Foundations of probability
Probability is a field of mathematics designed to formally reckon with the idea of chance. When you say “the chance of drawing an ace, given that you’re holding one, is 5.4%”, you’re using probability. But critically, although probability was developed with this applied, “real world” goal in mind, it rests on a pure mathematical footing just like a less applied field like number theory.
Let’s take a tour through this footing. Probability first assumes we are dealing in some space of possible events where we can measure (loosely: quantify) the probability of each event. Call a specific event E and its probability P(E). (So for example, if our space is die rolls, then there are 6 events.)
Then we lay out 3 axioms, first set by Kolmogorov:
The probability of a possible event occurring is a non-negative, non-imaginary number.
The probability of something happening is 100%. (Or if you prefer, 1. Same thing. 100 per centum = 100 per 100 = 1.) For example, if you have a 6-sided die, the probability you roll some number, any number, 1 thru 6 is 100%.
The probability of some combination of multiple, non-overlapping events happening is the same as the sum of their individual probabilities. For example, the probability of rolling a 2 or a 6 is the same as P(rolling a 2) + P(rolling a 6).
These concepts should all strike you with the feeling of: um, duh? That’s why they’re great axioms!
Again, remember that we are accepting these axioms as truth without need for evidence or proof of any kind. For example, we’re not going to try to list out every infinite possible set of events, measure their probabilities, and verify the axioms above hold. That would be inductive, the realm of empirical science, and we’re not in that game. In fact, it might not even be correct to say these axioms are “true” — they’re just, accepted without question as starting assumptions.
An easy little theorem
Let’s use the axioms to derive a wee theorem on complements.
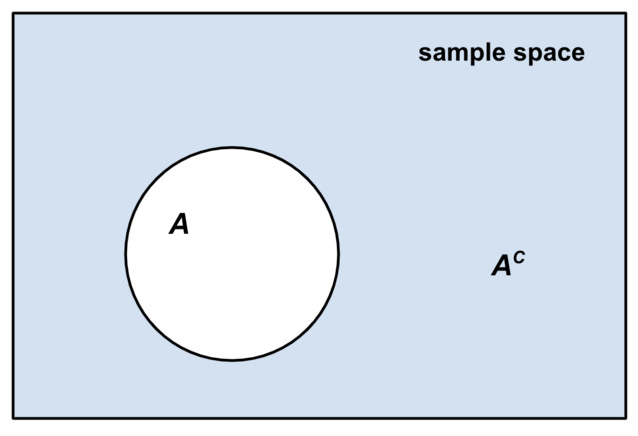
Definition. Consider a set of events A, which is a subset of all possible events Ω. Then define the complement of the set A, which we’ll call Ac, as all the events in Ω that aren’t in A. We can represent this visually with:
Note, by definition, A joined with Ac is equal to Ω. In math notation, we can write this fact as A ∪ Ac = Ω. As an example, if Ω is die rolls, we could have A be rolling 1 thru 3, and then Ac would be 4 thru 6.
We’ve defined a new term, let’s see if we can deduce something about it using the axioms. Consider this proposition:
Theorem. P( Ac ) = 1 - P(A).
Or in words, the probability of everything but A happening is equal to 1 less the probability of A happening. This makes intuitive sense, maybe, since we know Ac and A are non-overlapping sets of events that together describe all possible events, so it seems the probability of Ac and the probability of A should all add up to 1 (the probability of something happening).
In fact, this intuition guides us to a more formal proof:
Proof. We know that A and Ac together make Ω, or A ∪ Ac = Ω, by definition. Therefore, we know that P(A ∪ Ac) = P(Ω). (follows from the definition)
Next, recall that P(Ω) = 1. (from Axiom 2)
Also, recall that the overall probability of events from A or Ac is equal to the sum of the probability of the individual sets. That is, P(A ∪ Ac) = P(A) + P(Ac). (follows from Axiom 3)
Finally, notice that our definition from the start of the proof, together with these two deductions from Axioms 2 and 3, allows us to say:
P(A) + P(Ac) = P(Ω) = 1 and therefore P(Ac) = 1 - P(A).
And to really drive it home, let’s do an …
Example. Consider the question: if we flip a coin 5 times, what’s the probability of getting at least one heads? Computing this directly is surprisingly tricky — think of all the possible sequences you’d have to account for! TTTHT, TTTHH, HTHTH, etc etc.
Instead, let’s use our theorem we just proved. Let Ω represent all possible sequences of flipping a coin 5 times. Let A represent the event of tossing zero heads, and then Ac represents tossing at least one heads. We see that A consists of a single possible sequence: TTTTT. Since this is one sequence out of 2^5 possible, its probability must be 1 over 2^5=32, or 1/32 (about 3%). Therefore,
P(tossing at least one heads) = 1 - P(tossing no heads) = 1 - (1/32) = 96.8%.
Reflections and wonder
This sequence of definitions, theorem statement, proof (intermixed with appeals to intuition), example … this is a common pattern in mathematics. I absolutely love it. I think it is such a clean form of exposition, and I wish its form were followed in more disciplines. How many arguments could be resolved by just agreeing on definition of terms? How much confusion could be settled with a well-posed example?
This pattern of setting down a small number of self-evident-seeming axioms, and proceeding to deduce progressively more complex theorems from these axioms using strict logic, is a foundational pattern in all mathematics. This type of constructive, deductive, formal (but intuitive) creation is so exciting and something I wanted to highlight as an essential part of “true” mathematics.
I’m curious how the proof of the complement struck you:
It may have seemed inscrutable — the logic didn’t follow, the substitutions of terms didn’t make sense — and if so, I’d ask you to try giving it another read (or two, or five). Math is very dense — there is a lot of information packed into a small space.
A more common reaction is that it seems overkill — the theorem statement already seemed true, why bother with this pedantic proof? I don’t blame you; this is a very simple theorem, so it almost seems evident from the definition, without proof. But math is a strict discipline — we should progress deliberately from axiom to theorem, minding all the little fiddly bits, and showing our work along the way. If we get fast and loose, we might miss an edge case or exception.
Overall, I find this little journey in demonstrating the foundations of probability as a peek into how all mathematical disciplines start. It’s exciting, in its own way, to see 3 axioms begin to sprout theorems, like a flowering garden.
Further reading
For more lay-friendly math, may I recommend various YouTube channels like Numberphile or 3Blue1Brown, or math3ma. In the written world, Quanta magazine does a Herculean job of balancing technical accuracy with accessibility, but it’s focused on emerging topics and errs on the side of engaging narrative, not necessarily learning. There are many, many outstanding math blogs but most are written for mathematicians: Terry Tao, John Carlos-Baez, Scot Aaronson, Gwern Branwen, …
For the next post, I’ll probably keep up the chance theme and do something on random processes. Let me know your thoughts!